mathetutor

In einem kartesischen Koordinatensystem sind die Gerade

$g: \vec x =\left(\begin{array}{c} 6 \\ 4\\ 3\end{array}\right) + r\left(\begin{array}{c} 3\\ 1\\ -1,5\end{array}\right)$

und die Ebene

$E:\vec x = \left(\begin{array}{c} 3\\ 3\\ 0,5\end{array}\right) + p\left(\begin{array}{c} 6\\ 0 \\ -2\end{array}\right)+q \left(\begin{array}{c}3\\ -1 \\ -0,5\end{array}\right)$

gegeben.

Bestimme $E\cap g$ .
Bestimme eine Gleichung der Ebene $E^*$ , die zu $E$ parallel ist und $g$ enthält.
Ermittle den Abstand von $E$ zu $E^*$ .
Bestimme die Schnittpunkte $A,B$ und $C$ von $E$ mit den Koordinatenachsen.
Die Gerade $f$ steht senkrecht auf $E$ und geht durch den Punkt P(11/5/5). Liegt der Schnittpunkt von $f$ und $E$ innerhalb des Dreiecks ABC?

Lösung folgt.

Erster Post und gleich ein so hochgegriffenes Thema: Grenzwerte. Der ein oder andere mag das Thema noch aus der Schule kennen, irgendwie musste man sich damit befassen, aber irgendwie auch nicht, weil viele Probleme, in denen der Grenzwert eine Rolle spielt, doch letztlich nur auf eine Formel oder ein möglichst einfaches Lösungsverfahren reduziert werden.

Aber was ist so ein Grenzwert überhaupt? Nun, einfach gesprochen geht es beim Grenzwert um die Frage was passiert, wenn ich mich einem bestimmten Wert nähere, ohne ihn wirklich zu erreichen. Das kann man mit Folgen, Funktionen, usw. machen. Eigentlich mit allem, das das dynamische Auswerten von Eingaben ermöglicht. Ich möchte mich an dieser Stelle auf Folgen reduzieren, sicherlich aber in dem ein oder anderen Artikel oder Beispiel auch auf andere Grenzwerte eingehen.

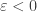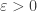Was bedeutet es mathematisch eigentlich, einer Zahl sehr nahe zu kommen, sie aber nie zu erreichen? Nun, sicherlich kennt jeder den kürzesten Mathewitz der Welt: Sei $\varepsilon <0$ .

Der kleine griechische Buchstabe $\varepsilon$ ist sehr beliebt unter Mathematikern um auszudrücken, dass man eine sehr kleine Zahl wählen möchte, die aber nicht Null ist. Wenn also später die Rede von „sei $\varepsilon >0$ “ ist, dann soll das heißen, dass wir uns beliebig Zahlen aussuchen, die größer als Null sind, aber möglichst klein sein sollen. Das können also z.B. Zahlen wie 0,0000001 oder 0,0000000000021 sein.

Kommen wir nun aber zur eigentlichen Definition. Eine Zahlenfolge ist eine Funktion von den natürlichen Zahlen auf die reellen Zahlen, die jeder natürlichen Zahl eine reelle Zahl zuordnet, kurz eine Abbildung $\mathbb N\rightarrow\mathbb R, a_n\mapsto x$ .

Das klingt vielleicht kompliziert, mein aber nichts anderes als dass wir mehr oder weniger beliebig Zahlen aneinander reihen wollen. Da wir uns natürlich nicht mit wild ausgedachten Zahlen beschäftigen wollen, werden wir im Folgenden nur Folgen betrachten, die einer gewissen Regelmäßigkeit folgen, d.h. denen eine Zuordnungsvorschrift zugrunde liegt. Sei z.B. 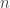$n$ eine natürliche Zahl, dann könnten wir 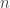$n$ bspw. stets seinen Kehrwert 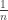$\frac{1}{n}$ zuordnen.

Haben wir eine solche Zahlenfolge gewählt können wir beliebig viele Folgenglieder bestimmen und werden manchmal feststellen, dass die Werte sich einem bestimmten Wert immer weiter nähern, ihn aber nie erreichen. Diese Zahl nennen wir Grenzwert.

Bilden wir bspw. für die Folge 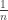$\frac{1}{n}$ einige Folgenglieder so stellen wir schnell fest, dass sie sich der Null immer weiter nähert, sie aber nie erreicht. Die Null ist Grenzwert der Zahlenfolge.

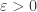Mathematisch formuliert bedeutet das: Sei $(a_n)$ eine Folge reeller Zahlen und $g\in\mathbb R$ . Sei $\varepsilon>0$ . Dann heißt $g$ Grenzwert der Zahlenfolge, wenn für alle 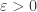$\varepsilon>0$ ein $n_0\in\mathbb N$ existiert, so dass für alle $n\geq n_0$ gilt $|a_n-g|<\varepsilon$ .

Das klingt auf den ersten Blick sehr kompliziert und umständlich und beinhaltet, was den Nicht-Mathematiker sicherlich am meisten stört, nicht einmal ein Rezept wie man den Grenzwert einer Folge denn nun bestimmen kann. Die Definition setzt schlichtweg voraus, dass wir bereits wissen, wie der Grenzwert unserer Folge aussieht. Dies ist auch meist das Hauptproblem, der Beweis ist dann eher ein Trick-17-Beweis, indem man rückwärts rechnet, aber vorwärts aufschreibt.

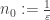Für unser Beispiel $a_n=\frac{1}{n}$ gilt bspw.: $\left|\frac{1}{n}-0\right|=\frac{1}{n}<\varepsilon\Leftrightarrow \frac{1}{\varepsilon}<n$ . Wir wählen also $n_0:=\frac{1}{\varepsilon}$ und fertig. Das ist mathematisch zwar nicht ganz sauber, man müsste eigentlich noch etwas argumentieren, aber das soll uns an dieser Stelle nicht weiter interessieren.

Nun sind wir in der Lage zu zeigen, dass unsere Folge einen Grenzwert hat, sofern wir ihn denn kennen (über sog. Cauchy-Folgen könnten wir auch zeigen, dass unsere Folge konvergiert, d.h. einen Grenzwert hat, ohne diesen überhaupt zu kennen), aber wir wollen ja darauf hinaus, Grenzwerte zu berechnen bzw. geschickt zu raten, ohne erst Unmengen von Folgenglieder zu berechnen.

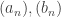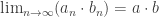Dazu sind uns die Grenzwertsätze ein gutes Hilfsmittel: Sind $(a_n), (b_n)$ Folgen, die geeigneten Voraussetzungen genügen, mit Grenzwerten $a,b$ , dann gilt, was man sicherlich vermuten würde: $\lim_{n\rightarrow\infty} (a_n+b_n)=a+b$ , $\lim_{n\rightarrow\infty} (a_n\cdot b_n)=a\cdot b$ , $\lim_{n\rightarrow\infty} \frac{a_n}{b_n}=\frac{a}{b}$ .

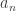Dabei soll $\lim_{n\rightarrow\infty} a_n=a$ bedeuten, dass die Folge $a_n$ den Grenzwert a hat, wenn wir 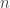$n$ gegen Unendlich schicken.

Mit Hilfe dieser Grenzwertsätze lassen sich viele Probleme auf Folgen zurückführen, deren Grenzwerte man recht schnell einsehen kann. Wir haben bereits gesehen, dass $(a_n)=\frac{1}{n}$ den Grenzwert 0 hat, analoges gilt für alle Folgen der Form $\frac{1}{n^k}$ mit $k\in\mathbb N$ beliebig. Man nennt diese Folgen Nullfolgen, weil sie gegen Null konvergieren.

Durch geschickte Umformungen lassen sich zumindest auf Ebene der Schulmathematik fast alle Folgen auf solche Folgen zurückführen, indem man z.B. geschickt ausklammert.

Betrachten wir bspw. die Folge $(a_n)=\frac{n^2+n-1}{2n^2+1}$ . Dann können wir durch Ausklammern der höchsten Potenz im Zähler und Nenner Nullfolgen konstruieren:

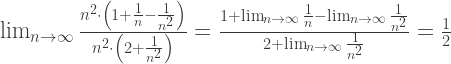$\lim_{n\rightarrow\infty} \frac{n^2\cdot\left(1+\frac{1}{n}-\frac{1}{n^2}\right)}{n^2\cdot\left(2+\frac{1}{n^2}\right)} = \frac{1+\lim_{n\rightarrow\infty}\frac{1}{n}-\lim_{n\rightarrow\infty}\frac{1}{n^2}}{2+\lim_{n\rightarrow\infty}\frac{1}{n^2}} = \frac{1}{2}$ , denn durch das Ausklammern von 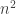$n^2$ und anschließendes Kürzen erhalten wir Nullfolgen, die bei der Grenzwertbildung eine Null geben.

Versuche doch selbst mal zu begründen, dass $\lim_{n\rightarrow\infty}\frac{n^2+2n-1}{n^3+2}=0$ .

Wozu aber nun das Ganze? Grenzwerte spielen in den mathematischen Theorien oft eine unsichtbare Rolle, für viele mathematische Begriffe nutzt man ihn, aber eigentlich sieht man ihn nicht, da er sich hinter anderen Begriffen versteckt. Ein Beispiel dafür ist die Ableitung. Man betrachtet hier Grenzwerte der Form $x\rightarrow x_0$ , kann daraus jedoch sehr schnell die Ableitungsregeln verifizieren und lässt den Grenzwert geschickt aus der Rechnung verschwinden. 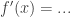Wenn ihr also schreibt $f'(x)=...$ ist das eigentlich nichts anderes als eine Grenzwertbetrachtung, die jedoch durch Rechenregeln vereinfacht worden ist.

mathetutor

Übung: Geraden, Ebenen und Abstände

Übung: Kurvendiskussion

Grenzwerte von Zahlenfolgen

Hello world!

Aktuelle Beiträge

Neueste Kommentare

Archiv

Kategorien

Meta